Mathematics is often seen as abstract, but when broken down, it becomes a practical tool to solve everyday problems. In this unit, we dive into two important branches – Analytical Geometry and Integration. Analytical geometry helps us understand the positions and relationships of points and lines in a plane, while integration allows us to calculate areas, volumes, and cumulative quantities. Together, these topics form a powerful foundation for advanced studies in mathematics, science, and engineering.

Introduction to Analytical Geometry
Analytical geometry, also called coordinate geometry, is a field of mathematics that examines geometric shapes and their properties using a coordinate system. It links algebra and geometry, allowing us to describe geometric shapes using algebraic equations and vice versa. This is done by placing geometric figures on a coordinate plane, which is formed by two perpendicular number lines: the x-axis (horizontal) and the y-axis (vertical). The point where they intersect is called the origin (0, 0).
Signs of the Coordinates
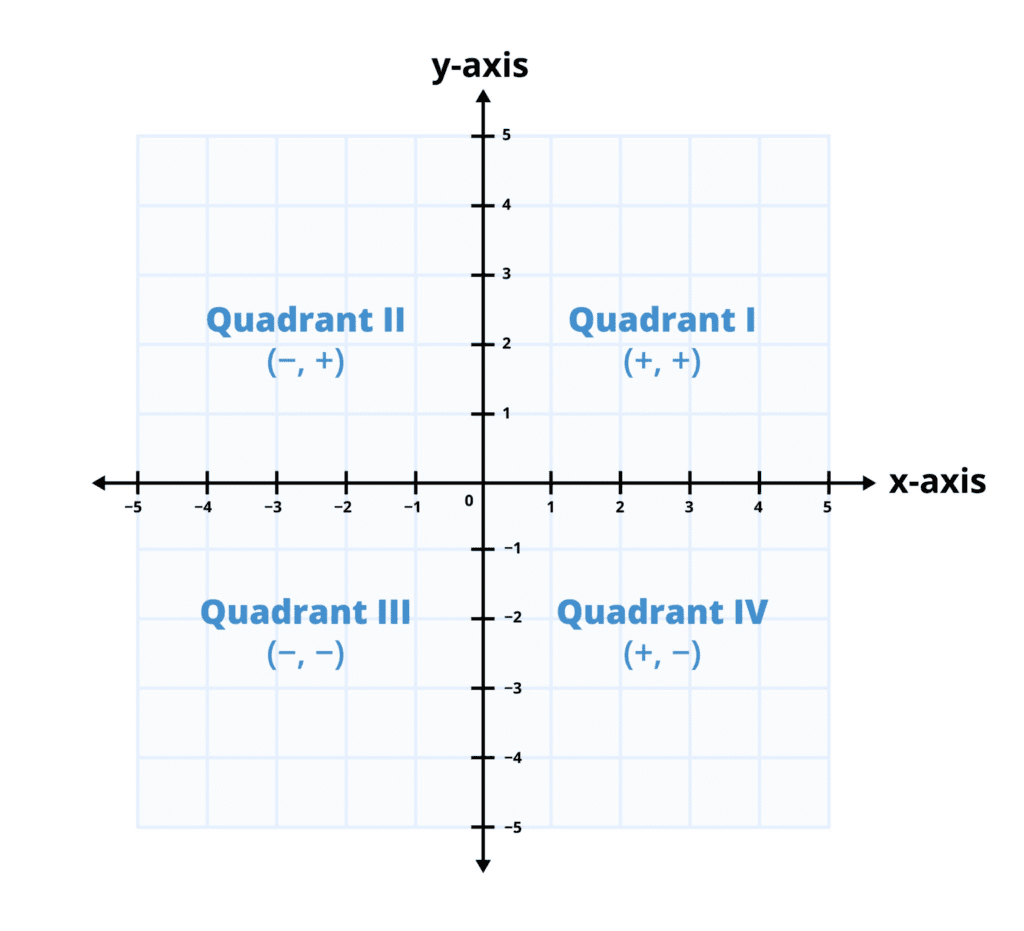
The coordinate plane is divided into four quadrants by the x-axis and y-axis. In each quadrant, the signs of the coordinates (x,y) follow a specific and consistent pattern:
- Quadrant I: (+,+) — Both the x-coordinate and y-coordinate are positive.
- Quadrant II: (−,+) — The x-coordinate is negative, and the y-coordinate is positive.
- Quadrant III: (−,−) — Both the x-coordinate and y-coordinate are negative.
- Quadrant IV: (+,−) — The x-coordinate is positive, and the y-coordinate is negative.
Slope or Gradient of a Straight Line
The slope (or gradient) of a straight line indicates how steep the line is. It is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. The slope is generally represented by the symbol m.
- A positive slope indicates that the line goes up from left to right.
- A negative slope indicates that the line goes down from left to right.
- A zero slope indicates a horizontal line.
- An undefined slope indicates a vertical line
Slope-Intercept Form of a Straight Line
The slope-intercept form is a common way to write the equation of a straight line. It is given by:
y=mx+c
- m is the slope of the line.
- c is the y-intercept, which is the point where the line crosses the y-axis (i.e., the value of y when x=0).
This form is useful because it directly gives you the slope and y-intercept of the line, making it easy to graph.
Example: The equation y=2x+3 represents a straight line with a slope (m) of 2 and a y-intercept (c) of 3. This means the line rises two units for every one unit it moves to the right and crosses the y-axis at the point (0, 3).
Introduction to Integration
Integration is a fundamental concept in calculus that is the inverse process of differentiation. It is used to find the area under a curve, the volume of solids, and to solve differential equations. The process of finding an integral is called integration.
Definition
An integral is the inverse of a derivative. If the derivative of a function F(x) is f(x), then the integral of f(x) is F(x). This is written as:
∫f(x)dx=F(x)+C
- ∫ is the integral sign.
- f(x) is the integrand.
- dx indicates that the integration is with respect to the variable x.
- F(x) is the antiderivative.
- C is the constant of integration, which is included because the derivative of any constant is zero.
Standard Formulae
Here are some basic integration formulae:

Application
Integration has vast applications in science, engineering, and pharmacy. In pharmacokinetics, for instance, integration is used to calculate the Area Under the Curve (AUC), which represents the total exposure of a patient to a drug over time. The AUC is a key parameter for determining drug bioavailability and bioequivalence. Integration is also used to model drug concentration in the body and to determine the rate of drug elimination.
